Пам’ятаєте, як у дитинстві ми складали кубики один на одного і рахували їх? Ця проста гра насправді пов’язана з важливим математичним поняттям. Куби чисел оточують нас всюди – від коробок на полицях магазинів до розрахунків інженерів при будівництві мостів. Ці математичні величини допомагають нам краще розуміти простір навколо нас.
Що таке куб числа?
Куб числа – це результат множення числа на себе тричі. Коли ми беремо число 2 і множимо його на себе тричі (2 × 2 × 2), отримуємо 8. Отже, 8 – це куб числа 2.
Термін “куб” з’явився невипадково. Якщо уявити квадрат зі стороною 2 см і “підняти” його вгору на 2 см, ми отримаємо куб з об’ємом 8 кубічних сантиметрів. Саме тому число 8 називають кубом числа 2.
Ми можемо уявити це так: квадрат – це число в другому степені (площа), а куб – це число в третьому степені (об’єм).
Формули та властивості кубів чисел
Формули та властивості кубів чиселКуб числа a записують як a³. Це означає, що число множиться на себе три рази: a³ = a × a × a.
Куби чисел мають цікаві властивості:
- Куб додатного числа завжди додатний. Наприклад, 2³ = 8 (додатне).
- Куб від’ємного числа завжди від’ємний. Наприклад, (-2)³ = -8 (від’ємне).
- Куб парного числа завжди парний. Так, 4³ = 64 – парне число.
- Куб непарного числа завжди непарний. Наприклад, 3³ = 27 – непарне число.
Коли ми піднесемо до куба число 1, отримаємо 1. А куб нуля завжди дорівнює нулю.
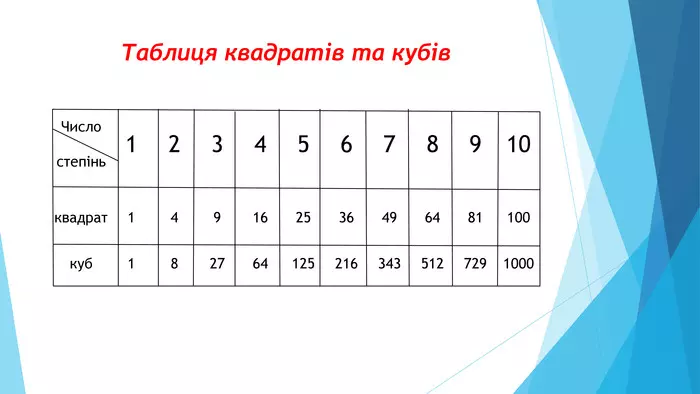
Таблиця кубів чисел
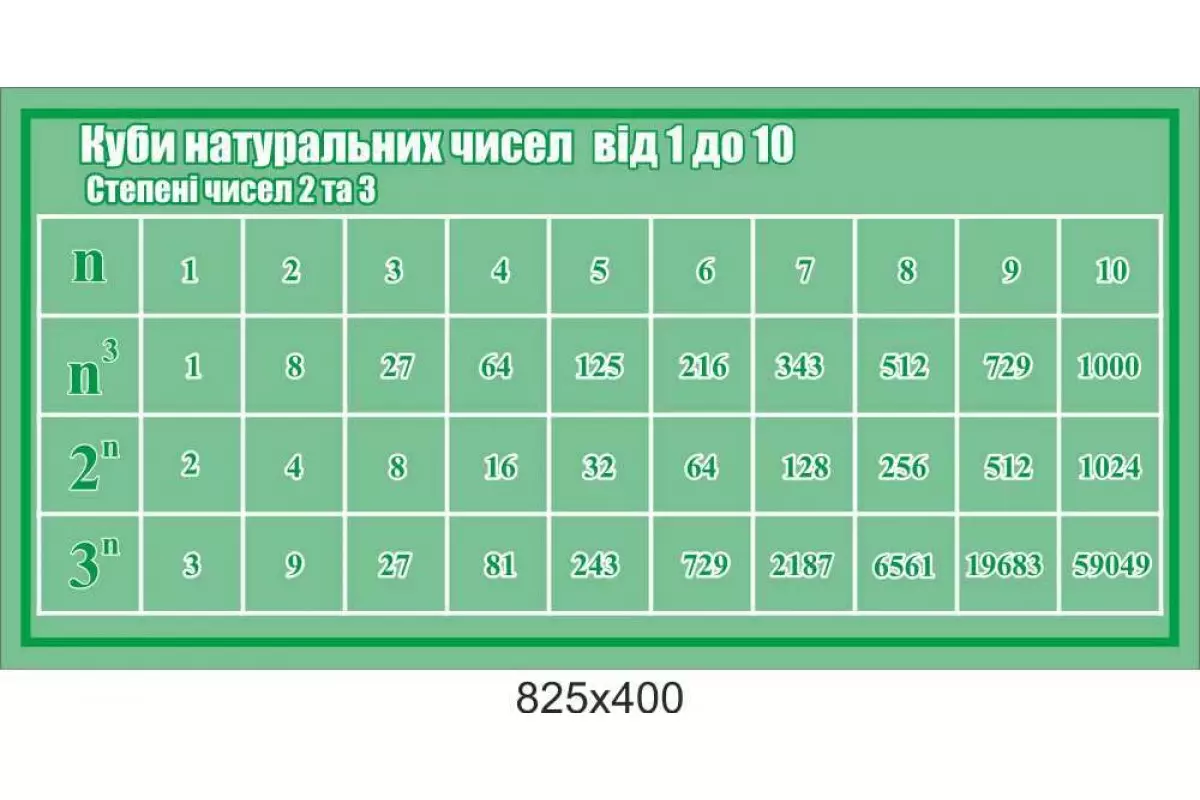
Знати куби перших десяти чисел корисно для швидких розрахунків:
| Число | Куб числа |
|---|---|
| 1 | 1 |
| 2 | 8 |
| 3 | 27 |
| 4 | 64 |
| 5 | 125 |
| 6 | 216 |
| 7 | 343 |
| 8 | 512 |
| 9 | 729 |
| 10 | 1000 |
Зверніть увагу, як швидко зростають значення кубів! Куб числа 10 вже дорівнює 1000, а куб числа 100 буде вже 1 000 000.
Практичне застосування кубів чисел
Куби чисел часто використовують у повсякденному житті, навіть якщо ми цього не помічаємо:
- Геометрія та будівництво. Коли будівельники рахують, скільки матеріалу потрібно для кімнати, вони множать довжину, ширину та висоту – це і є обчислення об’єму через куб.
- Фізика. Сила опору повітря зростає пропорційно кубу швидкості. Тому коли автомобіль їде вдвічі швидше, йому треба подолати у вісім разів більший опір повітря.
- Комп’ютерна графіка. У 3D-моделюванні куби чисел допомагають створювати об’ємні об’єкти та розраховувати їхні властивості.
У школі вам може знадобитися обчислення кубів для розв’язання рівнянь або при вивченні функцій. Спробуйте самі побудувати графік функції y = x³ і порівняйте його з графіком y = x².
Історичний контекст та цікаві факти
Давні греки розв’язували задачу “подвоєння куба” – як побудувати куб з об’ємом удвічі більшим за заданий. Ця задача виявилася настільки складною, що її змогли розв’язати лише через багато століть.
Цікавий факт: сума кубів перших n натуральних чисел дорівнює квадрату суми цих чисел. Наприклад, 1³ + 2³ + 3³ = (1 + 2 + 3)². Перевірте це самі!
Також математики знають, що будь-яке ціле число можна представити як суму не більше дев’яти кубів інших цілих чисел. Ця властивість знадобилася при розробці сучасних методів шифрування.
Куби чисел – це не просто математичні абстракції. Вони допомагають нам описувати реальний тривимірний світ навколо нас. Від простих обчислень об’єму кімнати до складних інженерних розрахунків – куби чисел завжди з нами.
Наступного разу, коли ви побачите кубик Рубіка або звичайну коробку, згадайте про куби чисел та їхні властивості. Математика ближча до повсякденного життя, ніж здається на перший погляд!
Пишу про все, що надихає та змушує задуматися. Маю журналістську освіту та багато років досвіду у створенні пізнавальних матеріалів. Захоплююсь наукою, культурою та історіями успіху. Шукаю цікаве в усьому, аби ділитися знаннями, які допомагають відкривати нові горизонти, бачити красу світу та отримувати корисні поради для життя.
