Кожен з нас хоч раз стикався з квадратами в житті — чи то плитка на кухні, чи шахова дошка, чи клаптик землі під будинок. Площа цих квадратів впливає на наше життя більше, ніж здається на перший погляд. Коли ми купуємо фарбу для стін чи шпалери, розраховуємо кількість плитки для підлоги, нам потрібно точно знати площу поверхні.
Що таке квадрат
Квадрат — це чотирикутник, у якого всі сторони рівні між собою, а всі кути прямі (90 градусів). Це одна з найпростіших геометричних фігур, яку ми часто бачимо в повсякденному житті.
Уявіть собі звичайний аркуш паперу з зошита в клітинку. Кожна клітинка — це квадрат. Всі сторони клітинки однакові, і кути між ними становлять 90 градусів.
Формула площі квадрата
Площа квадрата дорівнює квадрату довжини його сторони. Записуємо цю формулу так:
S = a²
де S — площа квадрата, а — довжина сторони квадрата.
Чому ця формула працює? Уявіть квадрат зі стороною 4 см. Ми можемо розділити його на 16 маленьких квадратиків зі стороною 1 см. Кожен такий квадратик має площу 1 см². Тому площа всього квадрата — 16 см².
4 × 4 = 16 см²
Це і є квадрат числа 4, тобто 4².
Приклади обчислення площі квадрата
Приклад 1: Квадрат має сторону 5 м. Знайдемо його площу. S = 5² = 5 × 5 = 25 м²
Приклад 2: Квадратний майданчик має сторону 12 м. Яка його площа? S = 12² = 12 × 12 = 144 м²
Приклад 3: Площа квадратної кімнати становить 36 м². Яка довжина її сторони? Якщо S = a², то a = √S = √36 = 6 м
Обчислення площі квадрата за діагоналлю
Іноді ми знаємо не сторону, а діагональ квадрата. В такому випадку можна використати іншу формулу:
S = d²/2
де d — довжина діагоналі.
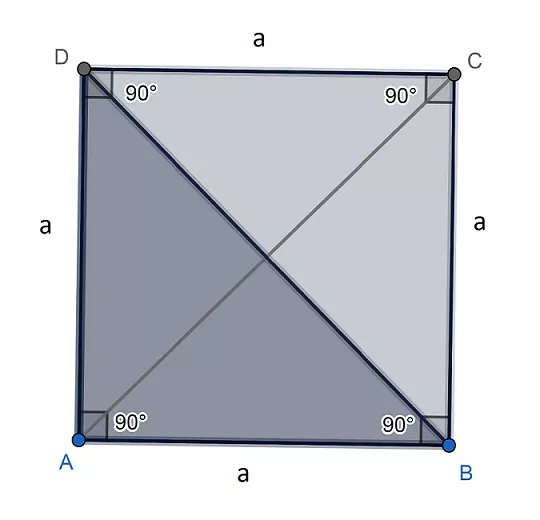
Ця формула випливає з теореми Піфагора. Діагональ квадрата ділить його на два рівні прямокутні трикутники. За теоремою Піфагора:
d² = a² + a² = 2a²
Звідси a² = d²/2, а оскільки S = a², то S = d²/2.
Приклад: Діагональ квадратного поля дорівнює 10 м. Знайдемо його площу. S = d²/2 = 10²/2 = 100/2 = 50 м²
Практичне застосування
Знання формули площі квадрата допомагає нам у багатьох життєвих ситуаціях:
При ремонті: розрахунок кількості фарби, шпалер, плитки- У будівництві: визначення кількості матеріалів для підлоги чи стелі
- У садівництві: планування грядок, клумб, газонів
- У побуті: вибір розміру килима, скатертини, рушника
При ремонті: розрахунок кількості фарби, шпалер, плиткиНаприклад, для фарбування квадратної стіни зі стороною 3 м потрібно знати її площу: S = 3² = 9 м². Знаючи, що одна банка фарби покриває 5 м², ми купимо 2 банки.
Поширені помилки при обчисленні площі
- Плутанина між площею та периметром. Периметр — це сума довжин усіх сторін (для квадрата P = 4a), а площа — це простір всередині фігури.
- Неточне вимірювання. Навіть маленька помилка у вимірюванні сторони призводить до більшої помилки в площі через квадрат числа.
- Неправильне використання одиниць вимірювання. Якщо сторона в метрах, то площа в квадратних метрах, а не просто в метрах.
Вміння обчислювати площу квадрата — базова навичка, яка стає в пригоді і школярам, і дорослим. Ця проста формула S = a² допомагає нам ефективно планувати простір і ресурси. Тож наступного разу, коли побачите квадрат, спробуйте швидко визначити його площу — ця навичка точно не буде зайвою у вашому математичному арсеналі.
Пишу про все, що надихає та змушує задуматися. Маю журналістську освіту та багато років досвіду у створенні пізнавальних матеріалів. Захоплююсь наукою, культурою та історіями успіху. Шукаю цікаве в усьому, аби ділитися знаннями, які допомагають відкривати нові горизонти, бачити красу світу та отримувати корисні поради для життя.
