Квадратне рівняння: як розв’язати просто і зрозуміло
Коли стикаєшся з квадратним рівнянням, часто здається, що це щось складне й заплутане. Але якщо подивитись уважніше, у ньому є чітка логіка — кожен символ має свій сенс, а формули, які спершу лякають, згодом починають працювати на тебе. Тож давайте розберемось, як розв’язати квадратне рівняння, зрозуміти його сутність і не боятися формул.
Що таке квадратне рівняння
Квадратне рівняння — це рівняння виду ax² + bx + c = 0, де a, b і c — звичайні числа, а a ≠ 0. Якщо a дорівнює нулю, це вже зовсім інше — лінійне рівняння. Тому головна ознака квадратного — наявність x².
Щоб уявити це на прикладі, згадайте просту задачу: ви кидаєте м’яч угору. Його рух описується саме квадратним рівнянням, тому що висота змінюється залежно від квадрата часу. Так математика пояснює життя — через форму параболи, яка показує траєкторію руху.
«Математика — це не набір правил, а спосіб зрозуміти закономірність у всьому, що нас оточує.»
Квадратні рівняння зустрічаються і в побуті: розрахунок площі, економічні задачі, навіть дизайн арок або мостів. Вони не лише про цифри — це про логіку.
 Як знайти дискримінант
Як знайти дискримінант
Щоб знайти корені, потрібно обчислити дискримінант (D). Його формула проста:
D = b² – 4ac
Від значення D залежить, скільки буде розв’язків:
якщо D > 0 — два різних корені;
якщо D = 0 — один, але подвійний корінь;
якщо D
Наприклад:
x² − 3x + 2 = 0 → D = 9 − 8 = 1 → два корені.
x² + 4x + 4 = 0 → D = 16 − 16 = 0 → один корінь.
x² + x + 1 = 0 → D = 1 − 4 = −3 → немає дійсних коренів.
Це схоже на сигнали світлофора: зелений — іди далі, жовтий — лише один шлях, червоний — зупинись, бо далі тільки уявна зона.
Коли тренуєшся часто, перевіряти дискримінант стає інтуїтивно просто. А ще це перший крок, який вчить терпінню — без поспіху, лише чітка логіка.
Формула коренів квадратного рівняння
Як тільки дискримінант знайдено, далі все будується за формулою:
x₁,₂ = (-b ± √D) / (2a)
Якщо D = 0, обидва корені збігаються:
x = -b / (2a)
Приклад:
x² − 5x + 6 = 0
D = 25 − 24 = 1
x₁ = (5 − 1)/2 = 2
x₂ = (5 + 1)/2 = 3
Отже, маємо два корені: 2 і 3.
Формула здається холодною, але вона діє безвідмовно. У ній є симетрія: одне рішення з «плюсом», інше з «мінусом». І в цьому є щось гармонійне — як у природі, де все має протилежність.
Інші способи розв’язання
Не завжди варто одразу бігти до формули. Є кілька простих методів, які працюють не гірше.
1. Розкладання на множники
Якщо рівняння має зручні коефіцієнти, можна знайти два числа, добуток яких дорівнює c, а сума — b.
Наприклад:
x² − 3x + 2 = 0
Шукаємо два числа: добуток 2, сума −3 → це −1 і −2.
Отже: (x − 1)(x − 2) = 0
x₁ = 1, x₂ = 2
Метод швидкий, якщо бачите зв’язок між числами. Але тренується він лише з практикою — як інтуїція у водія, що відчуває машину без приладів.
2. Виділення повного квадрата
Підходить, коли рівняння можна «вирівняти». Наприклад:
x² + 6x + 5 = 0
Переносимо 5: x² + 6x = −5
Додаємо 9 (щоб утворився квадрат): (x + 3)² = 4
x + 3 = ±2
x₁ = −1, x₂ = −5
Цей спосіб допомагає побачити геометрію рівняння — за ним стоїть парабола, вершина якої і є ключем до коренів.
3. Графічний підхід
Інколи простіше подивитись, ніж рахувати. Графік y = ax² + bx + c — це парабола.
Точки, де вона перетинає вісь X, і є коренями. Якщо не перетинає — розв’язків немає.
«Графік — це діалог між формулою і уявою. Коли бачиш, як вона рухається, розуміння приходить само.»
Після кожного способу варто зупинитись і спробувати розв’язати подібну задачу самостійно. Це не теорія — це навичка, яку відчуваєш руками, коли пишеш розв’язання олівцем.
Теорема Вієта
Є ще один зручний інструмент — теорема Вієта.
Вона каже, що якщо x₁ і x₂ — корені рівняння x² + bx + c = 0, то:
x₁ + x₂ = −b
x₁ × x₂ = c
Приклад:
x² − 3x + 2 = 0 → x₁ + x₂ = 3, x₁ × x₂ = 2
Як бачимо, це ті самі числа 1 і 2.
Теорема допомагає перевірити, чи правильно знайдено корені, і швидко складати рівняння з відомими коренями.
Коли вчишся помічати ці закономірності, математика починає виглядати як мова символів, що описує порядок світу. І навіть у рівняннях можна знайти красу.
 Практичні приклади
Практичні приклади
x² − 2x − 8 = 0
D = 4 + 32 = 36 → √D = 6
x₁ = (2 + 6)/2 = 4
x₂ = (2 − 6)/2 = −2x² + 4x + 4 = 0
D = 16 − 16 = 0
x = −22x² − 8x + 6 = 0
D = 64 − 48 = 16
x₁ = (8 + 4)/4 = 3
x₂ = (8 − 4)/4 = 1
Спробуйте придумати власний приклад і розв’язати його.
Не потрібно одразу правильно — головне зрозуміти логіку кожного кроку. З часом вона стає природною, як відчуття рівноваги.
Квадратне рівняння — це не просто формула з підручника. Це спосіб мислити структуровано.
Коли ви навчаєтесь розв’язувати такі задачі, мозок привчається бачити зв’язки — не лише в математиці, а й у житті.
Після кількох розв’язків ви почнете помічати закономірності скрізь — у русі, у рішенні проблем, у логіці рішень. І це найкраща користь від математики.
«Математика не для того, щоб рахувати. Вона для того, щоб розуміти.»

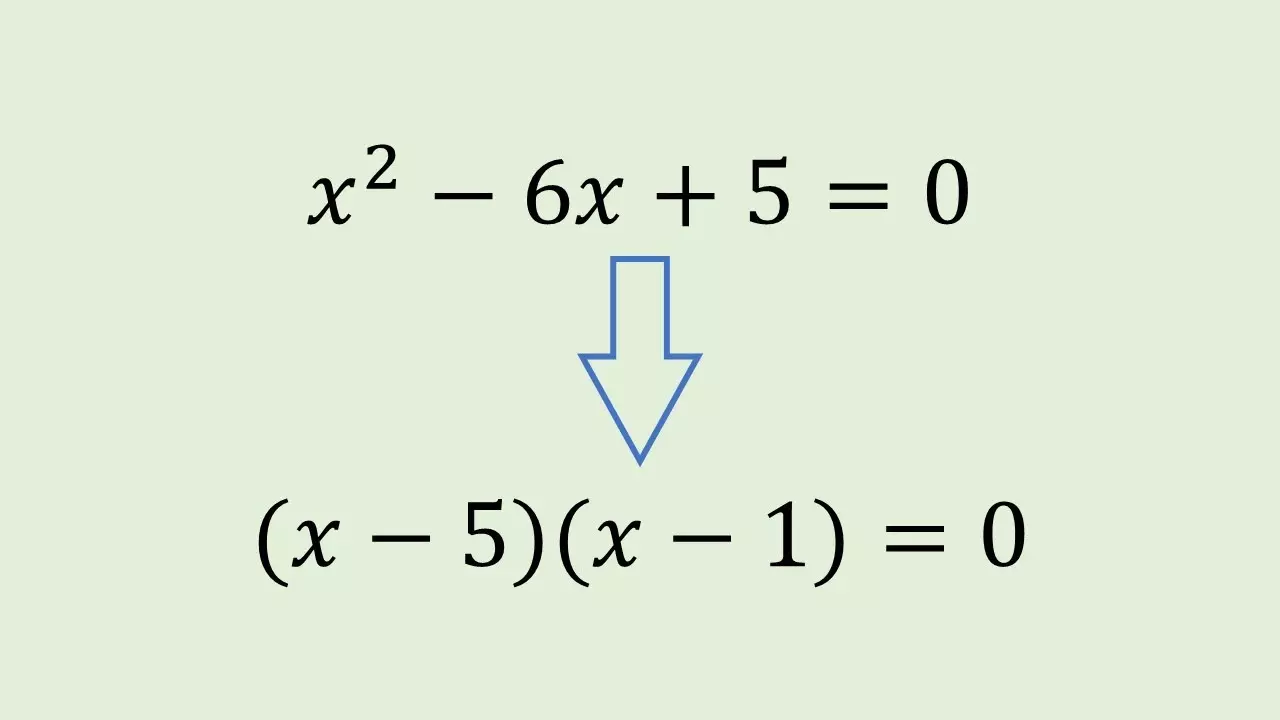 Як знайти дискримінант
Як знайти дискримінант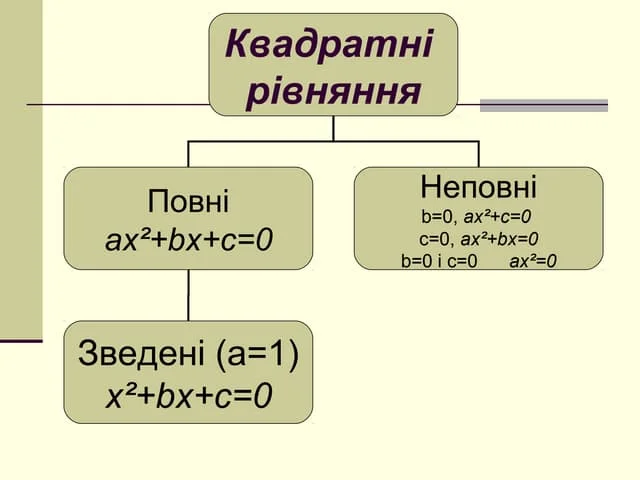 Практичні приклади
Практичні приклади