Що таке тангенс і як його використовувати в математиці

Пам’ятаєте шкільний урок, коли вчитель креслив на дошці трикутник і щось розповідав про синуси й косинуси? А потім з’явився він — загадковий тангенс. Для багатьох з нас ця функція залишилася таємницею, хоча ми користуємося її властивостями щодня — від будівництва сходів до розрахунку висоти дерев.

Що таке тангенс?

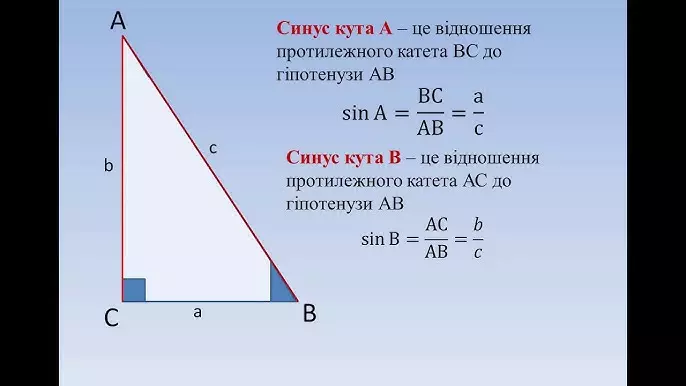
Тангенс — це одна з тригонометричних функцій, яка показує відношення довжин сторін у прямокутному трикутнику. Коли ми дивимося на прямокутний трикутник, тангенс кута — це відношення протилежного катета до прилеглого.

Формула проста: tg α = протилежний катет / прилеглий катет

Мій учитель математики пояснював це так: “Якщо ви стоїте біля підніжжя гори і дивитеся вгору під кутом 45°, то тангенс цього кута дорівнює 1. Це означає, що висота гори дорівнює відстані від вас до її підніжжя”.

У повсякденному житті ми використовуємо тангенс, коли вираховуємо, наскільки крутими мають бути сходи або схил даху. Кут нахилу сходів у звичайному будинку часто становить близько 30°, а тангенс цього кута приблизно 0,58.

Тангенс на одиничному колі

Тангенс можна зрозуміти ще краще через одиничне коло. Уявіть коло з радіусом 1, центр якого розташований у початку координат. Якщо ви проведете лінію від центра кола під певним кутом до осі x, тангенс цього кута буде довжиною відрізка від точки перетину цієї лінії з вертикальною дотичною до кола.

Це схоже на тінь, яку відкидає промінь світла на вертикальну стіну. Коли кут наближається до 90°, тінь стає все довшою і довшою, поки не стає безкінечною.

Властивості тангенса

Тангенс має кілька важливих властивостей:

• Він періодичний з періодом 180° (або π у радіанах). Це означає, що tg(α+180°) = tg(α).
• Функція тангенса непарна, тобто tg(-α) = -tg(α).
• Тангенс не визначений для кутів 90°, 270° і т.д., оскільки для них знаменник у формулі (прилеглий катет) дорівнює нулю.

Ось значення тангенса для деяких основних кутів:

• tg 0° = 0
• tg 30° = 1/√3 ≈ 0,577
• tg 45° = 1
• tg 60° = √3 ≈ 1,732

Коли я вчився будувати дах для садового будиночка, то використовував тангенс кута 30°, щоб розрахувати висоту підйому даху відносно ширини будинку.

Графік функції тангенса

Графік функції y = tg x виглядає як серія вертикальних кривих, які повторюються з періодом 180°. Ці криві наближаються до вертикальних ліній, які називаються асимптотами, але ніколи їх не перетинають.

Це схоже на американські гірки, які різко піднімаються вгору, але ніколи не перевертаються. Уявіть, що ви їдете на такому атракціоні — ваш шлях і буде графіком тангенса.

Функція тангенса не має обмежень на значення, які вона може набувати. Тангенс може бути як завгодно великим позитивним або негативним числом.

Застосування тангенса

Тангенс має багато практичних застосувань:

1. У будівництві — для розрахунку нахилу дахів, сходів, рамп. Наприклад, комфортний кут нахилу сходів — це 30-35°, що відповідає тангенсу приблизно 0,6-0,7.
2. У навігації — для визначення курсу руху. Коли штурман прокладає маршрут на карті, він використовує тангенс для визначення кута руху.
3. У фізиці — для розрахунку сил та траєкторій руху. Зокрема, при розв’язанні задач на похилу площину тангенс використовується для знаходження складових сили тяжіння.
4. В інженерії — для розрахунку опору матеріалів та конструкцій.

Приклади розв’язання задач

Задача 1: Знайти висоту дерева, якщо кут між лінією зору та горизонталлю становить 30°, а відстань від спостерігача до дерева — 20 метрів.

Рішення: Висота дерева = tg 30° × 20 м = 0,577 × 20 м ≈ 11,54 м.

Задача 2: Обчислити тангенс кута нахилу сходів, якщо висота сходового маршу — 3 м, а його горизонтальна проекція — 4 м.

Рішення: tg α = 3/4 = 0,75, що відповідає куту приблизно 37°.

Тангенс — це не просто абстрактне поняття з підручника, а інструмент, який ми використовуємо в повсякденному житті. Від будівництва даху до визначення висоти дерева — ця функція допомагає нам розуміти світ і вирішувати конкретні задачі.

Спробуйте подивитися навколо — і ви помітите тангенс у дії: у нахилі даху вашого будинку, в куті сходів, у схилі гірки в парку. Математика оточує нас скрізь, і знання тангенса робить нас більш підготовленими до розв’язання практичних задач.